【ML】机器学习概述与简单应用

什么是机器学习

直观视角下的机器学习

大众视角：

1

程序员视角：

2
2

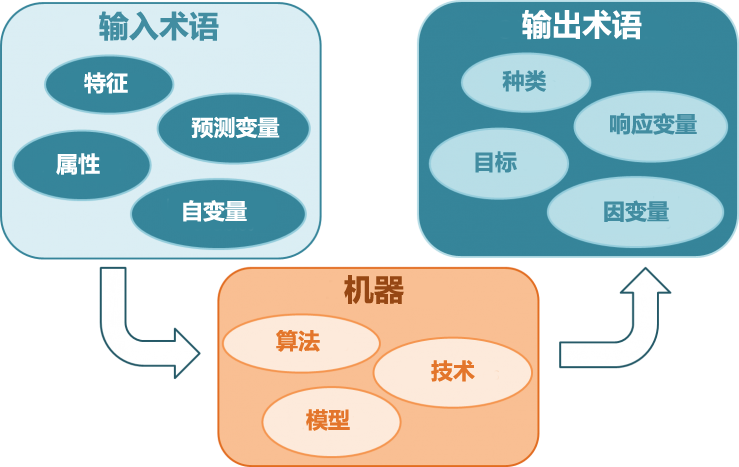
目前机器学习已经应用到了生活的各个方面。

百度搜索：其背后有这复杂的机器学习系统在努力地进行这个跟我们目标关键词相关的检索、排序工作；

美图、美拍这样的照相软件：使用了机器学习来识别面部并进行一定程度的美化；

垃圾箱里躺着的垃圾邮件：它们都不是我们主动拖拽移动进去的，而是机器学习帮我们自动地识别了垃圾邮件；

京东、天猫购物时，推荐的一些我们感兴趣的商品：促成我们更加便捷地购买，机器学习的推荐算法在其中发挥作用；

还有，新闻的推荐系统、语音识别、自然语言处理、无人驾驶、机器翻译等众多领域都有机器学习的影子。

维基百科：https://zh.wikipedia.org/wiki/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0

百度百科：https://baike.baidu.com/item/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0/217599

机器学习实际上是一门”教会”计算机学习而不需要明确地进行编程的科学。比如，扫地机器人，它应该怎样帮助我们清扫我们的房子呢？一种办法是让它学习我们如何清扫，让它看看我们都捡起了什么东西，然后把它们又放到什么地方，而不需要编写固定的程序让它们识别垃圾，并将它们移动到固定的垃圾桶。

机器学习——实际上在很多问题上都是一种通用解决方案。

它只需要通过大量的实例就可以以很高的精度逼近准确的解决方案。它带来的好处是不需要严格地去分析具体问题并构造精确解，它以一种通用的解决方案框架来对问题进行抽象建模，并通过大量的实例来纠正模型中的参数，并最终以该模型来逼近精确解，最终达到应用标准。

1-2

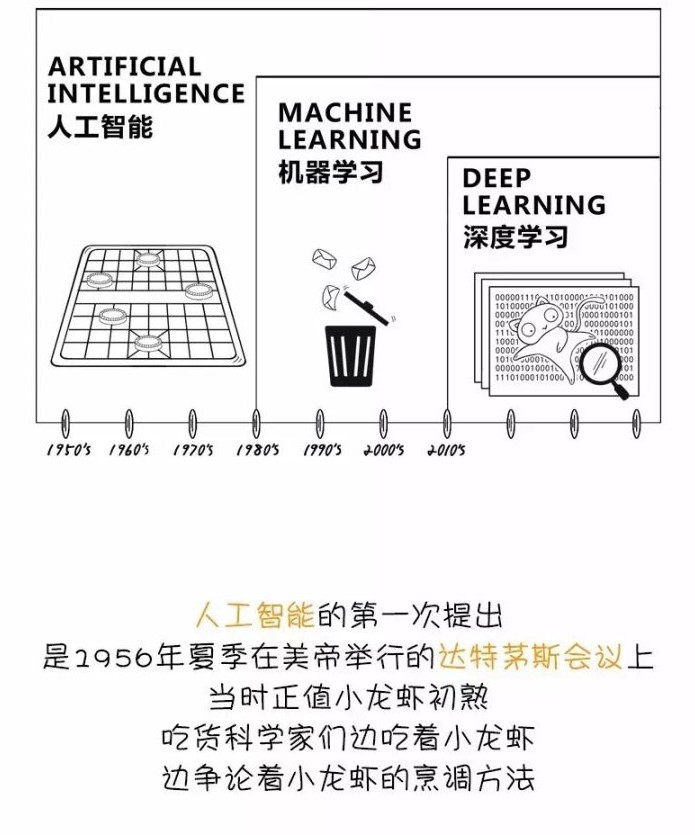
人工智能、机器学习与深度学习

2-1
2-2
2-3
2-4
2-5

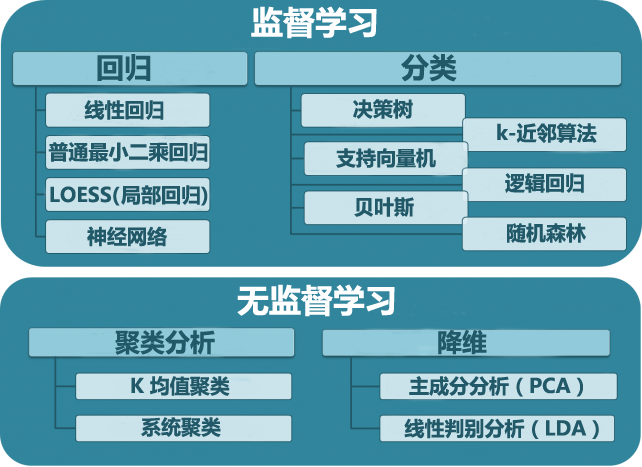
机器学习分类

机器学习根据训练方法大致可以分为3大类：

  1. 监督学习
  2. 非监督学习
  3. 强化学习

除此之外，大家可能还听过“半监督学习”之类的说法，但是那些都是基于上面3类的变种，本质没有改变。

监督学习

监督学习是指我们给算法一个数据集，并且给定正确答案。机器通过数据来学习正确答案的计算方法。

1-31
1-312

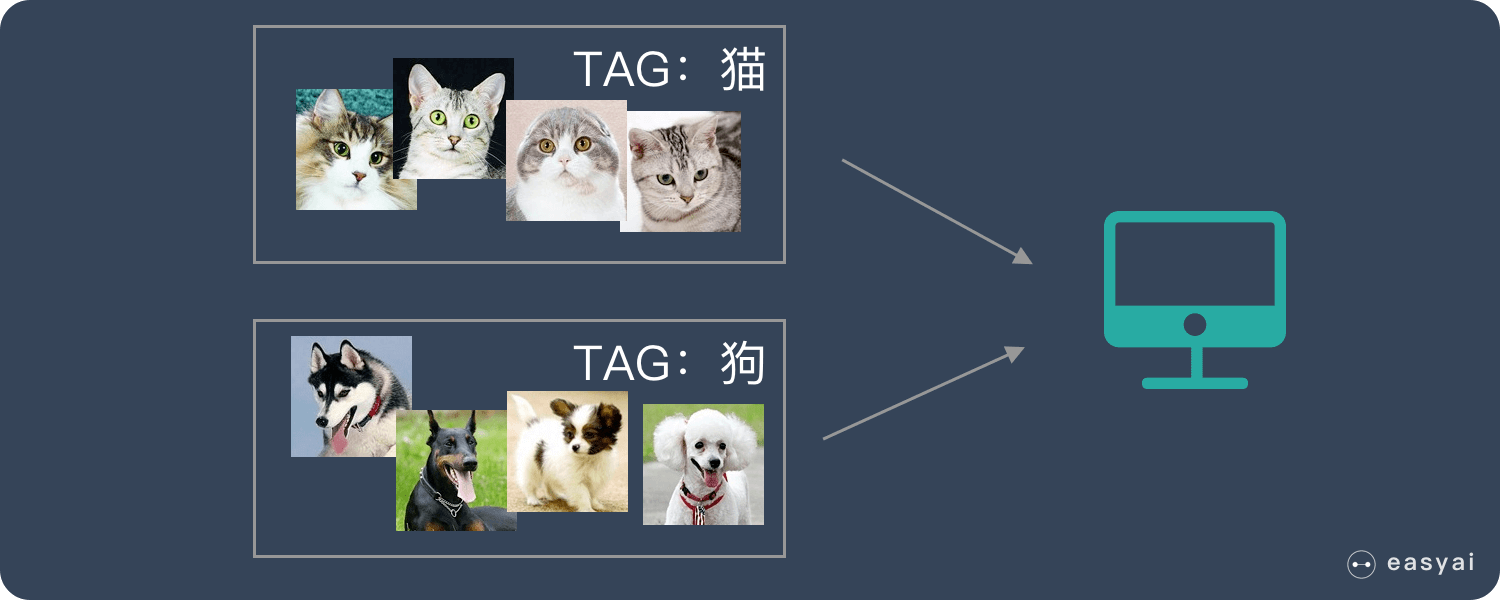
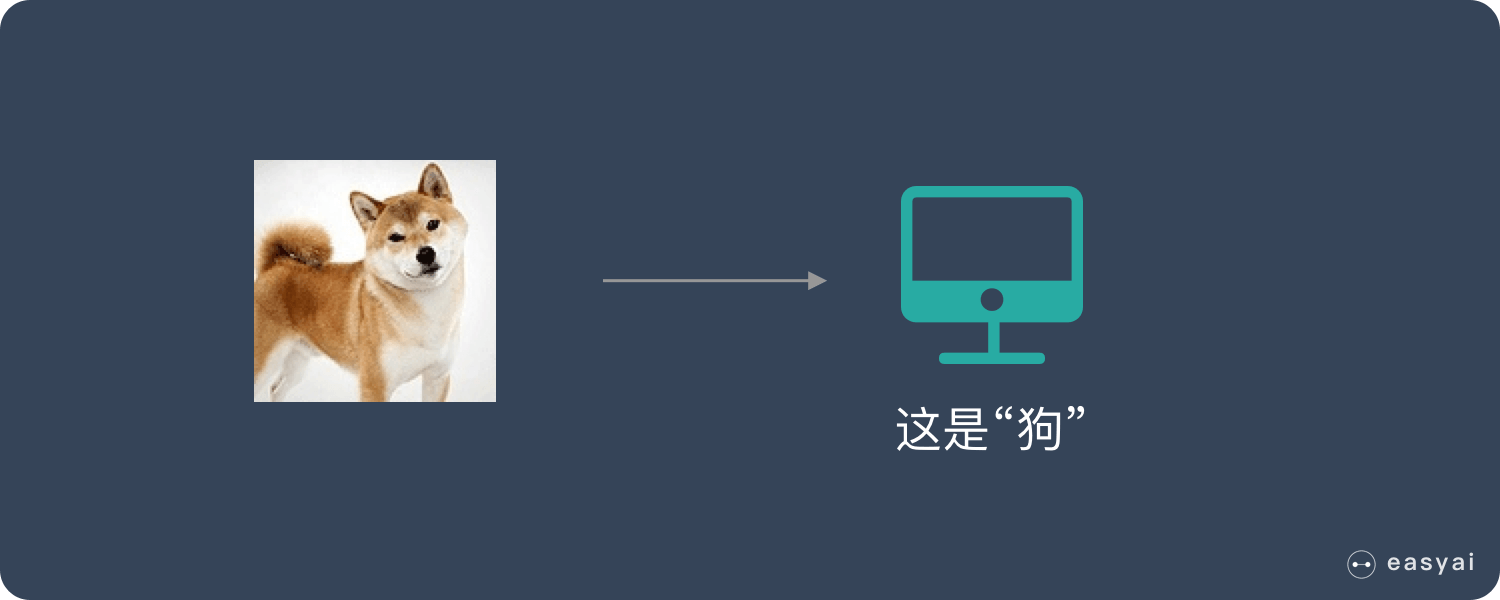
监督式学习采用分类和回归技术开发预测模型。

分类技术可预测离散的响应 — 例如，电子邮件是不是垃圾邮件，肿瘤是恶性还是良性的。分类模型可将输入数据划分成不同类别。典型的应用包括医学成像、语音识别和信用评估。

如果您的数据能进行标记、分类或分为特定的组或类，则使用分类。例如，笔迹识别的应用程序使用分类来识别字母和数字。在图像处理和计算机视觉中，无监督模式识别技术用于对象检测和图像分割。

回归技术可预测连续的响应 — 例如，温度的变化或电力需求中的波动。典型的应用包括电力系统负荷预测和算法交易。

如果您在处理一个数据范围，或您的响应性质是一个实数（比如温度，或一件设备发生故障前的运行时间），则使用回归方法。

非监督学习

非监督学习中，给定的数据集没有“正确答案”，所有的数据都是一样的。无监督学习的任务是从给定的数据集中，挖掘出潜在的结构。

1-32
1-322

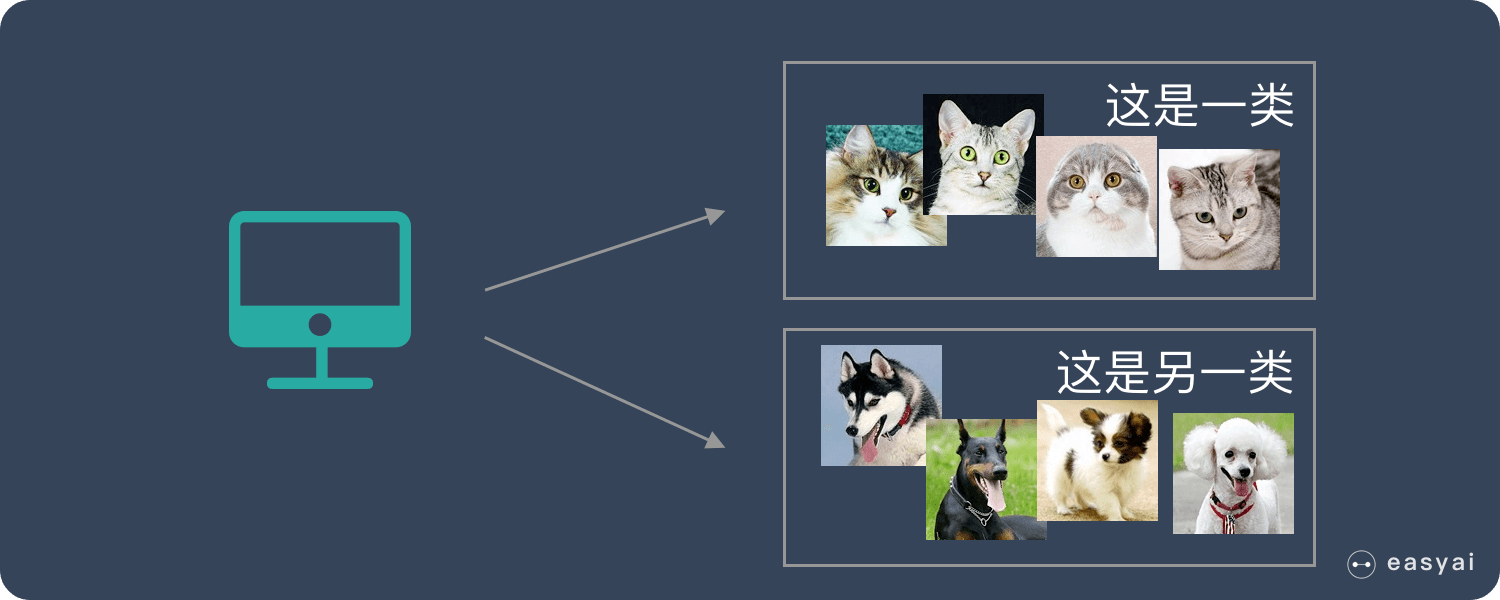
聚类是一种最常用的无监督学习技术。这种技术可通过探索性数据分析发现数据中隐藏的模式或分组。聚类分析的应用包括基因序列分析、市场调查和对象识别。

降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y，其中x是原始数据点的表达，目前最多使用向量表达形式。

目前大部分降维算法处理向量表达的数据，也有一些降维算法处理高阶张量表达的数据。之所以使用降维后的数据表示是因为在原始的高维空间中，包含有冗余信息以及噪音信息，在实际应用例如图像识别中造成了误差，降低了准确率；而通过降维,我们希望减少 冗余信息 所造成的误差,提高识别（或其他应用）的精度。又或者希望通过降维算法来寻找数据内部的本质结构特征。

强化学习

强化学习更接近生物学习的本质，因此有望获得更高的智能。它关注的是智能体如何在环境中采取一系列行为，从而获得最大的累积回报。通过强化学习，一个智能体应该知道在什么状态下应该采取什么行为。

1-33

怎样由数据和答案得到规则？

数据收集

公司历史数据积累
常见公开数据集

https://www.infoq.cn/article/zCGdpvyxJJl7*ja4RQAZ

https://zhuanlan.zhihu.com/p/34497496

网络爬虫

特征表达（去噪、特征提取与选择）

其实，说白了，就是我们人眼可见的特征转化为数字特征（可以用数学公式）的过程，并且这一过程是机器学习最重要的环节。

去噪：去除影响机器学习结果的原始数据。

分类变量特征提取：房价预测中房子的面积、朝向、位置、装修、楼层等等，它是标记的变量，不是连续的。

文字特征提取：很多机器学习问题涉及自然语言处理（NLP），必然要处理文字信息。文字必须转换成可以量化的特征向量。例如咱们公司的研发部算法组做的垃圾广告屏蔽器。

图片特征提取：做图像识别时，我们人眼看到的时图片，但是在机器中则是一个数字表示的二维矩阵。

数据标准化：主要用于对提取后的数字特征进行处理，因为提取好的数字特征可能会差距比较大，那么训练模型时，得到的特征权重会比较大或者比较小，同时也影响计算速度。

模型选择

选择正确的算法看似难以驾驭——需要从几十种监督式和非监督机器学习算法中选择，每种算法又包含不同的学习方法。

没有最佳方法或万全之策。找到正确的算法只是试错过程的一部分——即使是经验丰富的数据科学家，也无法说出某种算法是否无需试错即可使用。但算法的选择还取决于您要处理的数据的大小和类型、您要从数据中获得的洞察力以及如何运用这些洞察力。

3-31

模型训练

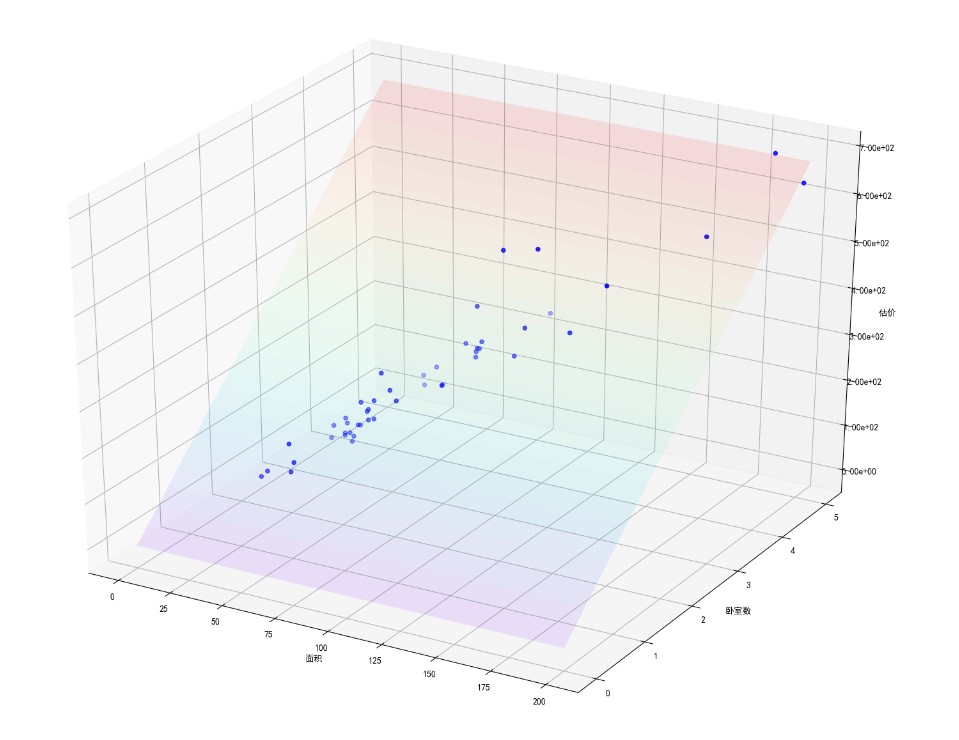
房价预测为例

3-4-1

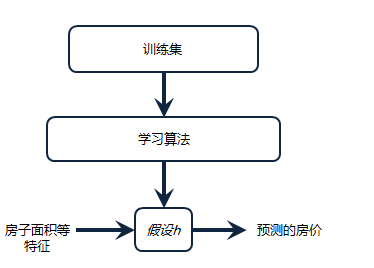
算法模型以简单多变量线性回归为例

面积(㎡) 卧室数 卫生间数 房龄 售价(百万元)
62.47 2 1 12 213
58.05 1 1 20 180
55.87 1 1 16 152
68.04 2 2 18 198
3-4-2

那么，这里的假设函数

3-4-3

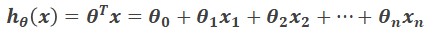
假设值与真实值之间的差就是这个模型的误差（代价）

3-4-4

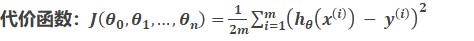
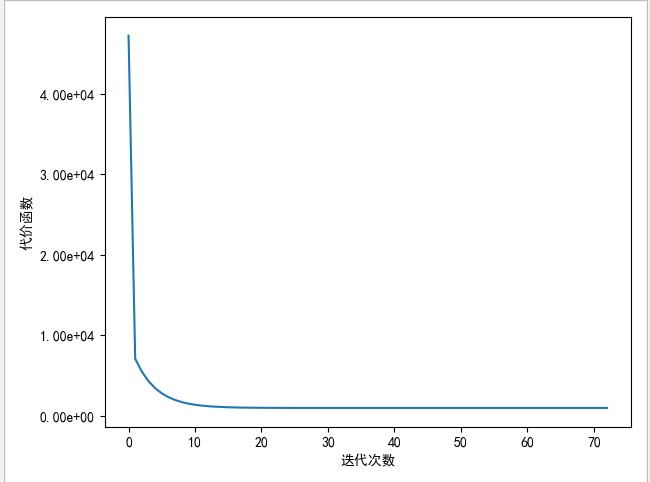
当代价函数的值趋近于0时，模型就比较完美了

参数调整

那怎样能是代价函数最小化？

梯度下降

共轭梯度

拟牛顿迭代法（BFGS）

L-BFGS

......

这里，我们已梯度下降法为例：

3-4-5

3-4-6

模型评估

对于分类问题：

正确率、召回率、F1值等等

3-4-8
3-4-7

对于回归问题：

3-6-3
3-6-4

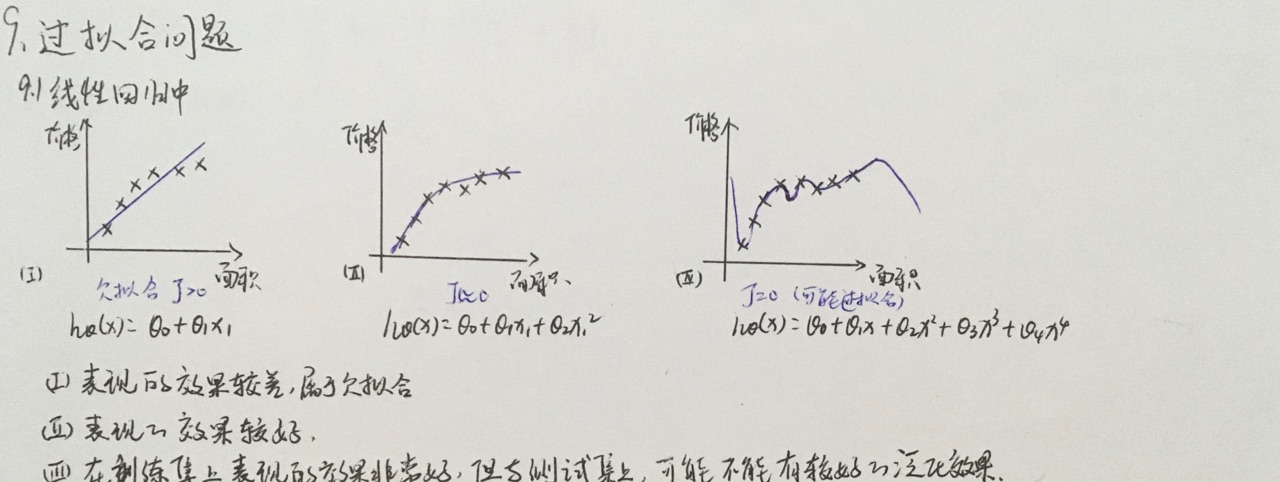
与过拟合对应的，就有欠拟合

实际预测

直接将样本参数带入h假设函数，便可以得到预测值

简单线性回归实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
import os
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.family'] = 'sans-serif'
matplotlib.rcParams['axes.unicode_minus'] = False
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cmimport matplotlib.ticker as mtick


def loadDataSet(filename):
    X = []
    Y = []
    with open(filename, 'rb') as f:
        for idx, line in enumerate(f):
            line = line.decode('utf-8').strip()
            if not line:
                continue

            eles = line.split()

            if idx == 0:
                numFea = len(eles)

            eles = list(map(float, eles))

            X.append(eles[:-1])
            Y.append([eles[-1]])
    return np.array(X), np.array(Y)


# 假设函数
def h(theta, X):
    return np.dot(X, theta)


# 代价函数
def J(theta, X, Y):
    m = len(X)
    return np.sum(np.dot((h(theta, X) - Y).T, (h(theta, X) - Y)) / (2 * m))


# 梯度下降更新公式
def bgd(alpha, maxloop, epsilon, X, Y):
    m, n = X.shape  # m是样本数，n是特征数(包括了全部是1的x0)，其实也就是参数theta的个数

    theta = np.zeros((n, 1))  # 参数theta全部初始化为0

    count = 0  # 记录迭代轮次
    converged = False  # 是否已经收敛的标志
    error = np.inf  # 当前的代价函数值
    errors = [J(theta, X, Y), ]  # 记录每一次迭代得代价函数值

    thetas = {}
    for i in range(n):
        thetas[i] = [theta[i, 0], ]  # 记录每一个theta j的历史更新

    while count <= maxloop:
        if (converged):
            break
        count = count + 1

        # 这里，我们的梯度计算统一了
        for j in range(n):
            deriv = np.dot(X[:, j].T, (h(theta, X) - Y)).sum() / m
            thetas[j].append(theta[j, 0] - alpha * deriv)

        for j in range(n):
            theta[j, 0] = thetas[j][-1]

        error = J(theta, X, Y)
        errors.append(error)

        if (abs(errors[-1] - errors[-2]) < epsilon):
            converged = True
    return theta, errors, thetas


def standarize(X):
    """特征标准化处理

    Args:
        X 样本集
    Returns:
        标准后的样本集
    """
    m, n = X.shape
    # 归一化每一个特征
    for j in range(n):
        features = X[:, j]
        meanVal = features.mean(axis=0)
        std = features.std(axis=0)
        if std != 0:
            X[:, j] = (features - meanVal) / std
        else:
            X[:, j] = 0
    return X


if __name__ == '__main__':
    data_set = os.path.dirname(os.path.abspath(__file__))+'/houses.txt'
    ori_X, Y = loadDataSet(data_set)  # 从南京链家抓取的夫子庙附近的房屋数据
    print(ori_X.shape)
    print(Y.shape)

    m, n = ori_X.shape
    X = standarize(ori_X.copy())
    X = np.concatenate((np.ones((m, 1)), X), axis=1)

    alpha = 1  # 学习率
    maxloop = 5000  # 最大迭代次数
    epsilon = 0.000001  # 收敛判断条件

    result = bgd(alpha, maxloop, epsilon, X, Y)
    theta, errors, thetas = result

    # 预测
    normalizedSize = (70 - ori_X[:, 0].mean(0)) / ori_X[:, 0].std(0)
    normalizedBr = (2 - ori_X[:, 1].mean(0)) / ori_X[:, 1].std(0)
    predicateX = np.matrix([[1, normalizedSize, normalizedBr]])
    price = h(theta, predicateX)
    print('70㎡两居估价: ￥%.4f万元' % price)

    # %matplotlib
    # 打印拟合平面
    fittingFig = plt.figure(figsize=(16, 12))
    title = 'bgd: rate=%.3f, maxloop=%d, epsilon=%.3f \n' % (alpha, maxloop, epsilon)
    ax = fittingFig.gca(projection='3d')

    xx = np.linspace(0, 200, 25)
    yy = np.linspace(0, 5, 25)
    zz = np.zeros((25, 25))
    for i in range(25):
        for j in range(25):
            normalizedSize = (xx[i] - ori_X[:, 0].mean(0)) / ori_X[:, 0].std(0)
            normalizedSize = (xx[i] - ori_X[:, 0].mean(0)) / ori_X[:, 0].std(0)
            x = np.matrix([[1, normalizedSize, normalizedBr]])
            zz[i, j] = h(theta, x)
    xx, yy = np.meshgrid(xx, yy)
    ax.zaxis.set_major_formatter(mtick.FormatStrFormatter('%.2e'))
    ax.plot_surface(xx, yy, zz, rstride=1, cstride=1, cmap=cm.rainbow, alpha=0.1, antialiased=True)

    xs = ori_X[:, 0].flatten()
    ys = ori_X[:, 1].flatten()
    zs = Y[:, 0].flatten()
    ax.scatter(xs, ys, zs, c='b', marker='o')

    ax.set_xlabel(u'面积')
    ax.set_ylabel(u'卧室数')
    ax.set_zlabel(u'估价')

    plt.show()

    errorsFig = plt.figure()
    ax = errorsFig.add_subplot(111)
    ax.yaxis.set_major_formatter(mtick.FormatStrFormatter('%.2e'))

    ax.plot(range(len(errors)), errors)
    ax.set_xlabel(u'迭代次数')
    ax.set_ylabel(u'代价函数')
    plt.show()
3-6-1
3-6-2
Machine Learning
#Python #ML
【ML】机器学习概述与简单应用
https://weitrue.github.io/2021/01/11/ml/
作者
Pony W
发布于
2021年1月11日
许可协议